Meta Açıklaması:
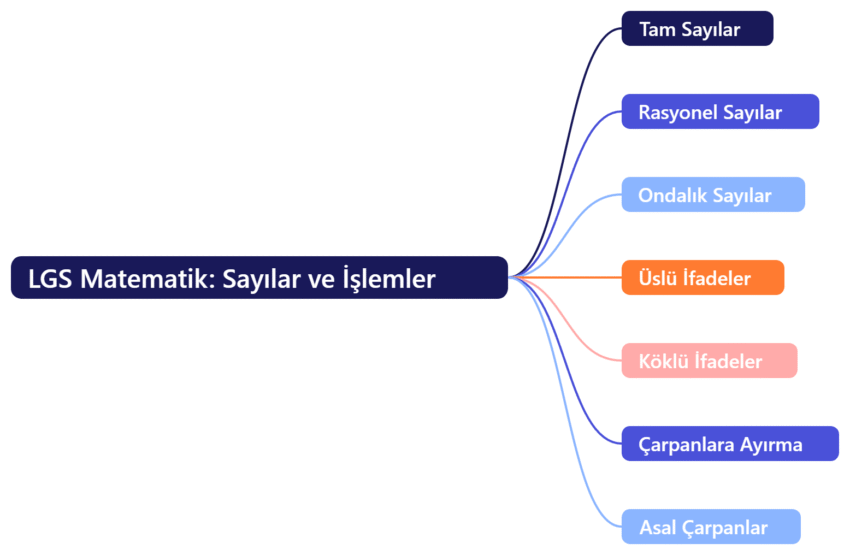
LGS matematik sayılar ve işlemler konusu tam sayılar, rasyonel sayılar, ondalık sayılar, üslü ve köklü ifadeler ile çarpanlara ayırma konularını detaylı ve anlaşılır şekilde öğrenin.
Giriş
LGS Matematik sınavında başarı sağlamak için sayılar ve işlemler konusunu iyi kavramak şarttır. Peki, tam sayılar, rasyonel sayılar, ondalık sayılar, üslü ifadeler, köklü ifadeler ve çarpanlara ayırma nasıl öğrenilir? Bu yazıda, bu temel konuları adım adım öğreneceksiniz. Ayrıca, sınavda karşınıza çıkabilecek örneklerle pratik yapma fırsatı bulacaksınız. Hazırsanız, başlayalım!
H2: Tam Sayılar ve Rasyonel Sayılar
H3: Tam Sayılar Nedir?
Tam sayılar, negatif ve pozitif tam sayılar ile sıfırı içerir. Örneğin, -5, 0, 7 tam sayılardır. Tam sayılar günlük hayatta sıcaklık ölçümü, borç-alacak hesapları gibi alanlarda kullanılır. Tam sayılarla toplama, çıkarma, çarpma ve bölme işlemleri yapılabilir.
H3: Rasyonel Sayılar Nedir?
Rasyonel sayılar, iki tam sayının birbirine bölümü şeklindedir. Örneğin, 3/4, -2/5, 7 tam sayısı da rasyonel sayıdır çünkü 7 = 7/1 olarak yazılabilir. Rasyonel sayılar kesirli sayıların genel adıdır ve sayı doğrusu üzerinde gösterilebilir.
H2: Ondalık Sayılar
H3: Ondalık Sayıların Tanımı
Ondalık sayılar, kesirlerin onluk tabanda yazılmasıdır. Örneğin, 3.14, 0.75 gibi sayılar ondalık sayılardır. Ondalık sayılar, özellikle ölçüm ve para hesaplarında sıkça kullanılır.
H3: Ondalık Sayılarla İşlemler
Ondalık sayılarla toplama ve çıkarma yaparken, virgülden sonra gelen basamak sayısı eşitlenir. Çarpma ve bölme işlemlerinde ise basamak sayısına dikkat edilir. Örneğin, 1.2 × 3.4 işleminin sonucu 4.08’dir.
H2: Üslü İfadeler
H3: Üslü İfadelerin Temel Kuralları
Üslü ifadeler, bir sayının kendisiyle tekrar çarpılmasıdır. Örneğin, ( 2^3 = 2 \times 2 \times 2 = 8 ). Üslü ifadelerde taban ve üs kavramları vardır. Taban çarpılan sayı, üs ise çarpma sayısını gösterir.
H3: Üslü İfadelerde İşlemler
Üslü ifadelerle işlem yaparken bazı kurallar geçerlidir:
- Aynı tabanlı üslüler çarpılırken üsler toplanır: ( a^m \times a^n = a^{m+n} )
- Aynı tabanlı üslüler bölünürken üsler çıkarılır: ( \frac{a^m}{a^n} = a^{m-n} )
- Üslü ifadenin üssü alınırsa üsler çarpılır: ( (a^m)^n = a^{m \times n} )
H2: Köklü İfadeler
H3: Köklü İfadelerin Anlamı
Köklü ifadeler, bir sayının kendisiyle kaç kez çarpıldığını gösteren üslü ifadenin tersidir. Örneğin, karekök ( \sqrt{9} = 3 ) çünkü ( 3^2 = 9 ). Karekök, küpkök gibi farklı kök türleri vardır.
H3: Köklü İfadelerle İşlemler
Köklü ifadelerde toplama, çıkarma, çarpma ve bölme işlemleri yapılabilir. Ancak, köklü ifadeler aynı radikallere sahip olduğunda toplanabilir veya çıkarılabilir. Örneğin, ( 3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2} ).
H2: Çarpanlara Ayırma
H3: Çarpanlara Ayırmanın Önemi
Çarpanlara ayırma, matematikte ifadeleri daha küçük ve çarpanlarına ayrılmış parçalara bölme işlemidir. Bu işlem, denklemleri çözmede ve işlemleri kolaylaştırmada büyük fayda sağlar.
H3: Çarpanlara Ayırma Yöntemleri
- Ortak çarpan parantezine alma: ( ab + ac = a(b + c) )
- İki terimli ifadelerde farkları: ( a^2 – b^2 = (a – b)(a + b) )
- Trinomların çarpanlara ayrılması: ( x^2 + 5x + 6 = (x + 2)(x + 3) )
H2: Asal Çarpanlar
H3: Asal Sayılar ve Asal Çarpanlar
Asal sayılar sadece 1 ve kendisine bölünebilen pozitif tam sayılardır. Örneğin, 2, 3, 5, 7 asal sayılardır. Bir sayının asal çarpanları, o sayıyı çarpanlarına ayırdığınızda elde edilen asal sayılardır.
H3: Asal Çarpanlara Ayırma İşlemi
Bir sayıyı asal çarpanlarına ayırmak için, o sayıyı en küçük asal sayılardan başlayarak bölmeye çalışırız. Örneğin, 60 sayısının asal çarpanları ( 2^2 \times 3 \times 5 ) şeklindedir.
H2: Örneklerle Pekiştirelim
| İşlem Türü | Örnek | Sonuç |
|---|---|---|
| Tam Sayılar | ( -3 + 7 ) | 4 |
| Rasyonel Sayılar | ( \frac{2}{3} + \frac{1}{6} ) | ( \frac{5}{6} ) |
| Ondalık Sayılar | 1.25 + 2.75 | 4.00 |
| Üslü İfadeler | ( 2^3 \times 2^2 ) | ( 2^5 = 32 ) |
| Köklü İfadeler | ( \sqrt{16} + \sqrt{9} ) | 7 |
| Çarpanlara Ayırma | ( x^2 – 9 ) | ( (x-3)(x+3) ) |
| Asal Çarpanlara Ayırma | 84 | ( 2^2 \times 3 \times 7 ) |
Sonuç
LGS Matematik sınavında sayılar ve işlemler konusu temel bir yapı taşını oluşturur. Tam sayılar, rasyonel sayılar, ondalık sayılar, üslü ve köklü ifadeler, çarpanlara ayırma ve asal çarpanlar konularını iyi anlamak, sınav başarınızı artırır. Bu konuları düzenli tekrar edip bolca soru çözerek pekiştirmenizi öneririz. Unutmayın, pratik yapmak bilgiyi kalıcı hale getirir!
Sık Sorulan Sorular (SSS)
Soru 1: Tam sayılar ve rasyonel sayılar arasındaki fark nedir?
Cevap: Tam sayılar sadece negatif ve pozitif tam sayılardır. Rasyonel sayılar ise tam sayıların birbirine bölünmesiyle oluşan kesirli sayılardır.
Soru 2: Üslü ifadelerde taban ve üs ne anlama gelir?
Cevap: Taban, kendisiyle çarpılan sayıdır; üs ise çarpma sayısını belirtir.
Soru 3: Köklü ifadelerde toplama nasıl yapılır?
Cevap: Sadece aynı radikallere sahip köklü ifadeler toplanabilir.
Soru 4: Çarpanlara ayırma neden önemlidir?
Cevap: İfadeleri daha basit parçalara ayırarak denklemleri çözmeyi kolaylaştırır.
Soru 5: Asal çarpanlara ayırma nasıl yapılır?
Cevap: Sayı, en küçük asal sayılardan başlayarak bölünür ve asal çarpanları bulunur.
SEO Başlığı
LGS Matematik Sayılar ve İşlemler Konuları Detaylı Anlatım
SEO Uyumlu URL
lgs-matematik-sayilar-ve-islemler
SEO Description
LGS matematik sayılar ve işlemler konusunu tam sayılar, rasyonel sayılar, ondalık sayılar, üslü ve köklü ifadelerle çarpanlara ayırma örnekleriyle öğrenin.
SEO Anahtar Kelimeler
LGS matematik, sayılar ve işlemler, tam sayılar, rasyonel sayılar, üslü ifadeler, köklü ifadeler, odak anahtar kelime: sayılar ve işlemler